こんにちは!
スロッターの皆さん、ジャグラー打ってますか?
ジャグラーは勝てないから打たない人、逆にジャグラーしか打たない人、ジャグラーは波を制した人が勝つ理論の人、いっぱいいると思います。
私は「ジャグラーは勝てる」派の人です。
というより現状、少なくとも大阪で稼働するのであればジャグラーは視野に入れておく方が収支は伸びると思います。
有名優良店には人が集まりますし、抽選勝負なところがありますからね。
ジャグラーは設定投入も何だかんだ高いですし、良い台が空く可能性も高いです。
さて、前置きはこのぐらいにして…


こんな人が多いのではないでしょうか?
台選びの根拠が間違っている。というわけではありません。
ジャグラーの勝ち方講座①でも書いた通り、ジャグラーにおいてREG確率を見ることは大切です。
ですが、ジャグラーの勝ち方講座②で書いた通り、REG確率という理由だけで座るのは良い台選びとは言えないのです。
今日はそんなお話です。
REG確率のブレについて考えてみる
マイジャグラーのREG確率
みんな大好きマイジャグラーを例にして、REG確率について考えていきましょう。
マイジャグラーのボーナス確率、機械割は下記表のようになっています。
| 設定 | BIG | REG | 合算 | 機械割 |
|---|---|---|---|---|
| 1 | 1/287.4 | 1/431.2 | 1/172.5 | 96.6% |
| 2 | 1/282.5 | 1/364.1 | 1/159.1 | 99.0% |
| 3 | 1/273.1 | 1/341.3 | 1/151.7 | 101.2% |
| 4 | 1/264.3 | 1/292.6 | 1/138.9 | 104.3% |
| 5 | 1/252.1 | 1/277.7 | 1/132.1 | 107.1% |
| 6 | 1/240.9 | 1/240.9 | 1/120.5 | 111.6% |
んー何度見ても魅力的な設定6の機械割
それはそうと今回注目すべきはREG確率
設定1で1/431 設定2で1/364になります。
印象としては設定2のREG確率が軽いなと思います。
例えばアイムジャグラーだと設定1で1/455 設定2で1/442です。
アイムジャグラーに比べて、設定1と2の差が著しいですね。
REG確率が1/300より良くなる確率を考える

さて、これについて考えていきましょう。
設定1を3000G回した時に1/300を切る確率(10回以上REGを引く確率)は16.52%になります。
え?っとなった方、思ったより大きい確率だったのではないでしょうか。
16.52%といえばだいたい1/6。設定1の6台に1台は3000G回して1/300以上のREG確率となってしまうのです。
これが設定2となると、32.24% 実に3台に1台が1/300を切ることになります。
この結果から言わしてもらうと、3000GでREG確率が1/300を切っているマイジャグラーに座る。という行動は愚かという他ないでしょう。
ただ、これもサンプルゲーム数が増えると話が変わってきます。
5000Gサンプルであれば、設定1であれば8%ほどでしか1/300を切ることはないです。ですが、設定2であれば23%で起こってしまいます。
ホールで設定2が一番使われているという理由はこう言ったところにあるのでしょう。
結局1/300という基準はどうなのか?
個人的に言わしてもらうと、論外です。
1/300を基準にしている人は設定1のREG確率にとらわれすぎだと思います。
設定2,3の可能性を考えるのであれば、1/300というラインは何G回っていようと設定すべき基準ではないと考えています。

こう考えた方もいらっしゃるのではないでしょうか。
この考え方は、確率の学習の時に出てきた「同様に確からしい」事象に対してのみ適用される考え方です。
すいません、難しく言いました。笑
要は、ホール内のジャグラーの設定が1~6まで均一に配分されている。という仮定でのみ成り立つ考え方だということです。
そんなことないですよね? ホール内の設定はほとんど1か2、設定6にいたっては無い可能性すらあります。
例えばホール内の20台のジャグラーが全て設定1だとしても、3台はREG確率1/300を切ってくるわけです。
このような状況下で1/300を基準にするというのは、良い判断ではないとわかっていただけたかと思います。
REG確率を見るのであればいくつを基準にすればよいか
では、結局REG確率を見るのであれば何分の1を基準にすればよいのでしょうか。
個人的な基準としては、REG確率のみを見るのであれば、3000Gサンプルで1/241(設定6のREG確率)を切っていてほしいですね。
3000G、1/241という基準であれば、設定1であれば2.6%、設定2であれば8%でしか起こりません。
あと3000Gといたサンプルゲーム数にこだわる人がいますが、私はそこは気にしていません。
例えば1000GでREG10回を引いている台であれば座ります。
これは設定1であれば0.06%でしか起こらないからです。
結局のところ、今起きている現象に対して、設定1なら何%か?設定2なら何%か?っと考えていって、「さすがに低設定であるとは考えにくい」と自分で納得で来たら打ち出します。
REG確率だけで打つことはしない
ここまで書いてきた全てを否定する見出しになってしまいました。
そもそもですが、私はREG確率だけを根拠にジャグラーを打つことはありません。
ジャグラーの勝ち方講座②~複数の理由を持とう~で書いた通り、ジャグラーを打つにはホール状況などの別の理由を付け加えて考えます。
ジャグラー単品で設定判別をするのは、よっぽどいい動きをしてくれないと不可能だと思います。
その理由としては、設定2のREG確率が1/364とそこまで大きく離れていないので、よほどブッチぎったREG確率でない限り根拠にはなりえないからです。
結論としては、REG確率を見ている人が負けている理由は2つです。
① 基準とするREG確率が緩い
② そもそもREG確率だけを基準にして打つことは間違い
ジャグラーの勝ち方講座を書いていますので、どうぞ参考にしていただければと思います。
参考 計算方法
ここからは別に読まなくても大丈夫ですが、この記事を見て「設定1で3000Gで1/300を切る確率とか、どう計算してるの?」っと思った方がいるのでは?っと思ったので計算方法について書いていこうかと思います。
これは、高校数学の数学Aの知識である2項分布を用いて計算することができます。
例えば、1/20の当たりくじを6回引いて2回当たりが出る確率は?という計算は二項分布を用いて計算できます。
下記が2項分布の式であり、上記例であれば n = 6(試行回数) k = 2(当たり回数) p = 1/20(当たり確率) q = 19/20(ハズレ確率)
![]()
パチスロの確率に当てはめると、3000G回して(n = 3000) REG(p = 1/431) を 10回引く(k = 10) 確率となります。
ここで重要なのは、この式は10回引く確率であって10回以上引く確率でなはないということです。
これを計算するには累積密度の考え方が必要になります。
要は 3000G回して11回引く確率,3000G回して12回引く確率、13回引く確率、14回引く確率…と3000回引く確率まで足し合わせる必要があるのです。
この計算は非常に面倒です。
よって下記サイトにアクセスして、条件を指定しましょう。
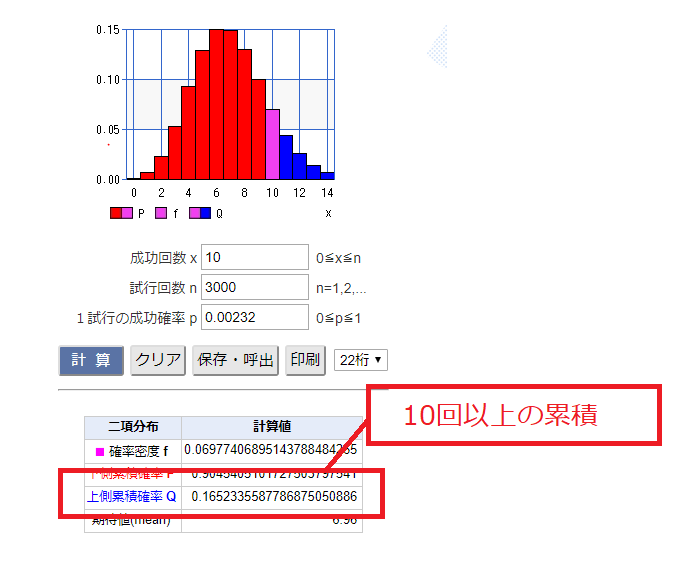
注意点としてはREG確率1/431は小数に直す必要があります。(1/431 = 0.00232 )
このようにして ○千ゲームで△分の1の確率を□回引く確率というのを計算しています!